Accretion of discount is the gradual increase in the value of a financial instrument over time. This occurs when the instrument’s interest payments are reinvested at a higher rate than the original investment’s coupon rate. As a result, the instrument’s value grows, or accretes, over time.
What is Accretion of Discount?

Discounts are a common financial tool used to incentivize early payments or to account for the time value of money. When a bond is issued at a discount, the proceeds received by the issuer are less than the face value of the bond. The issuer must then make periodic interest payments, called accruals, until the bond matures when the face value is paid back in full.
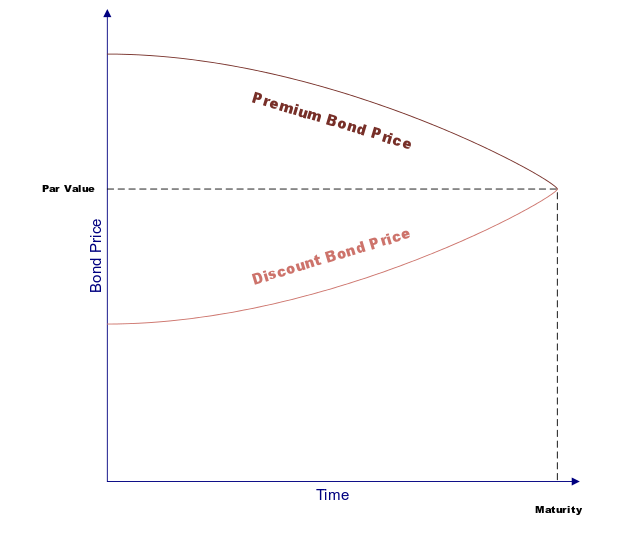
The accretion of discount is the gradual increase in the market value of a bond that is selling at a discount. As interest accrues on the bond, the market value of the bond increases until it reaches par value at maturity. The rate of accretion is equal to the coupon rate divided by the number of years to maturity.
For example, assume a $1,000 bond has a coupon rate of 6% and 10 years remaining until maturity. The market value of the bond today is $ 950.00. Each year, $60 in interest will accrue and be added to the market value of the bond until maturity when the total market value will equal $1,000. The annual rate of accretion would be 6% ($60/$950).
When Does Accretion of Discount Occur?

Discount accrual is the periodic interest that is earned on a bond between the last coupon payment date and the date of maturity. For example, if a bond has a 6% coupon rate and matures in 10 years, the investor will earn $60 per year in interest payments. The discount accrues at a rate of $6 per year, so at the end of 10 years, the investor will have earned $60 in interest payments and $60 in discount accrual.
How to Calculate the Accreted Value on a Perpetual Growth Annuity

To calculate the accreted value on a perpetual growth annuity, you need to first determine the periodic payment amount. This can be done by solving for the present value of an ordinary annuity formula for an annuity that pays out forever.
Once you have the periodic payment amount, you need to calculate the discount rate. The discount rate is the rate at which money grows over time, and is typically the same as the interest rate.
With the periodic payment amount and the discount rate, you can then calculate the accreted value of the annuity by using the following formula:
Accreted Value = Periodic Payment Amount / Discount Rate
For example, let’s say that you have an annuity that pays $100 per year and has a discount rate of 5%. The accreted value of this annuity would be $2,000.
Examples to See Accretion of Discount in Action

Discounts are present in many different types of transactions and can take on many different forms. The accrual of discount is the process by which the value of a discount is recognized over time. This can happen in a number of ways, but some common examples include:
-A bond that is issued at a discount will have its value increase over time as it approaches maturity. This is because the market value of the bond will increase as the interest payments come due, and the face value of the bond will be paid when it matures.
-A loan that is issued at a discount will also have its value increase over time as the interest payments are made. This is because the market value of the loan increases as the payments are made, and the face value of the loan will be paid when it is repaid in full.
-A investment that is made at a discount will also have its value increase over time as the underlying asset appreciates in value. This is because the market value of the investment will increase as the asset appreciates, and the face value of the investment will be paid when it is sold.
What Is Accretion of Discount? – Accretion of Discount Financial Definition
Accretion of discount is the gradual increase in the present value of a bond due to the compounding of interest. The effect of accretion is to reduce the yield to maturity of the bond.
When a bond is issued, it typically sells at a price that is less than its par value. The difference between the price and the par value is called the discount. For example, if a bond has a par value of $1,000 and sells for $950, the discount on the bond is $50.
The yield to maturity (YTM) of a bond is the rate of return that an investor will earn if they hold the bond until it matures. For example, if a bond has a YTM of 5%, an investor who buys the bond for $950 and holds it until it matures will earn 5% on their investment.
However, because bonds typically make periodic interest payments, an investor who buys a bond at a discount will receive more than their initial investment back in interest payments. As a result, the YTM of a discounted bond will be lower than the coupon rate.
For example, consider a bond with a par value of $1,000 that pays interest semi-annually at a rate of 6%. The bond sells at a discount of 10%, which means that it sells for $900. The YTM of this bond would be 4.17%.
The accretion of discount is the gradual increase in